- Unidad anterior
- ¿Qué es una Dimensión?
- EXAMEN DE CONCIENCIA
- SESION 16 - DIMENSIÓN Y BASES
- Material complementario.
- Anexo
- Algebra Lineal (Zoom)
- SESION 17 - TRANSFORMACIONES LINEALES
- Material Complementrario
- Anexo
- Algebra Lineal (Zoom)
- SESION 18 - TALLER!!
- EJERCICIOS DE REFUERZO
- JUEGOS DEL HAMBRE
- TALLER!!!
- Anexo (Taller)
- Taller (Zoom)
- Tercer Examen Parcial
- Siguiente unidad
JUEGOS DEL HAMBRE
4.1
Re: 4.1
Me queda muy claro el desarrollo que haces para obtener el determinante pero una pregunta porque sustituyes si el determinante es diferente de cero ya con eso sabemos que los vectores son lineal mente independientes.
:)
Re: 4.1
no entendi la pregunta XD
Re: 4.1
jajajaja no bro solo una sugerencia jajaja digo igual no se si estoy bien pero por que sustituyes y igualas las ecuaciones para saber que es
linealmente independiente si con que el determinante sea diferente de cero ya se sabe que son LI
Re: 4.1
Ya entendi XD, calcule el rango, de hecho para saber si es linealmente independiente , necesitas sacar el rango, con solo calcular la determinante lo que haces es saber cuantas lineas o renglones son linealmente independientes, supongamos que te da un 1 en la determinante, el resultado correcto seria que solo hay una linealmente independiente
Re: 4.1
Quedo muy bien tu procedimiento y el resultado, solo que no entiendo cómo calculaste el rango, ¿podrías explicarmelo?
Re: 4.1
claro, la manera de calcularlo es calcular primero el determinante, ya que lo tengas y sepas que es diferente de 0 tendra un rango >= a su dimensión ejemplo una matriz de 2x3 podemos decir que su rango es R=2 o R<=3 , y después ya todo seria visual con tu matriz para ver que una linea sea o no sea linealmente dependiente, como por ejemplo:
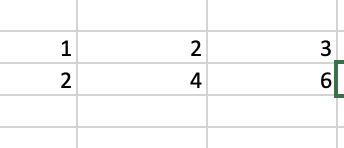
aqui hay dependencia lineal por que si la primer linea la multiplicas por 2 obtienes la segunda , entonces esta matriz seria linealmente dependiente