- Unidad anterior
- Presentación
- PLANEACIÓN DEL CURSO
- SESIÓN 01: Presentación del Curso.
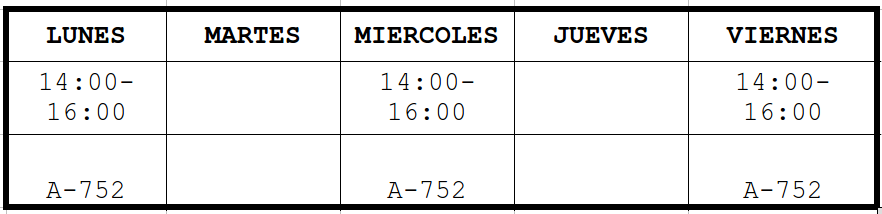
- Horario de sesiones en ZOOM
- Mapa de las matemáticas
- Geometría del plano y el espacio (revisited)
- Plano Cartesiano
- Dudas, quejas, sugerencias AQUI!
- Sesion 02: Geometría (revisited)
- Orden del día: 13 de mayo, 2020
- Material Adicional
- Algebra Lineal (Zoom)
- ¿Ya recordaste tu pregunta? Comentala aquí
- Sesión 03: Sistemas de Ecuaciones lineales.
- Algebra Lineal (Zoom)
- Ejemplos: Ecuaciones lineales
- QUIZ: Geometría euclidiana y sistemas de ecuaciones lineales
- An Interview with Gilbert Strang
- TAREA 1: Geometría Euclidiana, Sistemas de Ecuaciones Lineales
- Siguiente unidad
PLANEACIÓN DEL CURSO

NOMBRE DE LA UEA: ÁLGEBRA LINEAL I
CLAVE DE LA UEA: 4601093
TRIMESTRE: 20-I
GRUPO: CDO1-MA
El Álgebra Lineal es el centro de las matemáticas aplicadas modernas. Sus orígenes se remontan a la resolución de sistemas elementales de ecuaciones lineales algebráicas. Pero su más reciente objetivo es más vasto, al grado de afectar diversas disciplinas de las matemáticas, puras y aplicadas, como análisis numérico, estadística, ciencia de datos, física, ingeniería, matemáticas financieras y cada otra disciplina que requiera metodos matemáticos.
PRERREQUISITOS: GEOMETRIA (4601114) Y ALGEBRA SUPERIOR II (4601085)
OBJETIVO GENERAL
Al final del curso tendrás la capacidad de aplicar las herramientas del Álgebra lineal a problemas reales asociados con tu área de formación y distintas áreas de la ingeniería y las ciencias naturales.
OBJETIVOS ESPECÍFICOS
Plantearás y resolverás problemas mediante sistemas de ecuaciones lineales, empleando distintas técnicas, principalmente operaciones con matrices.
Comprenderás los conceptos algebráicos de ESPACIO VECTORIAL, BASES DE UN ESPACIO y TRANSFORMACIONES LINEALES.
Podrás realizar demostraciones de resultados elementales del Álgebra Lineal.
CONTRIBUCIÓN AL PERFIL DE EGRESO
Como alumno, serás capaz de desarrollar las habilidades para emplear el pensamiento abstracto y realizar demostraciones. Desarrollarás un lenguaje formal, criterio y pensamiento lógico, relacionarás datos y podrás interpretarlos como un sistema de ecuaciones o como un objeto matricial. Desarrollarás modelos matemáticos empleando elementos del Álgebra Lineal.
PROGRAMACIÓN TEMÁTICA POR SEMANA (TENTATIVA, SUJETA A CAMBIOS)
-
-
-
- Semana 1-4: Repaso de elementos de la geometría plana y del espacio. Sistemas de ecuaciones lineales, Matrices y determinantes.
- Semana 5-6: Aplicaciones.
- Semana 7-8: Espacios vectoriales
- Semana 9-10: Transformaciones Lineales.
-
-
RECURSOS NECESARIOS
Usaremos la plataforma UbiCua para compartir contenidos y material de apoyo, se crearán foros de discusión y Chats. Usaremos la aplicación ZOOM y BIG-BLUE-BUTTON para tener video-conferencias en tiempo real.
MODALIDADES DE CONDUCCIÓN
Desarrollar una cultura de enseñanza-aprendizaje que valore la argumentación, elaboración y prueba de modelos y exploración de los conceptos matemáticos del curso, así como su importancia en la respuesta a problemas prácticosen las ciencias naturales e ingeniería. Se fomentará al alumno en la resolución de problemas de forma individual así como la colaboración grupal y la participación en foros de discusión.
SISTEMA DE EVALUACIÓN
Se aplicarán exámenes quincenales de acuerdo al siguiente calendario.
- 1er examen parcial - 23 de mayo (semana 2).
- 2o. examen parcial - 6 de junio (semana 4).
- 3er. examen parcial - 20 de junio (semana 6).
- 4o. examen parcial - 4 de julio (semana 8).
- 5o. examen parcial - 11 de julio (semana 9).
- Entrevista - 13 de julio (semana 10).
- Examen Global - 15 de Julio (semana 10).
Se tomarán en cuenta también las actividades en la plataforma UbiCua. Se realizará una entrevista al final del curso.
En el caso que tu calificación no sea aprobatoria se presentará una evaluación Global.
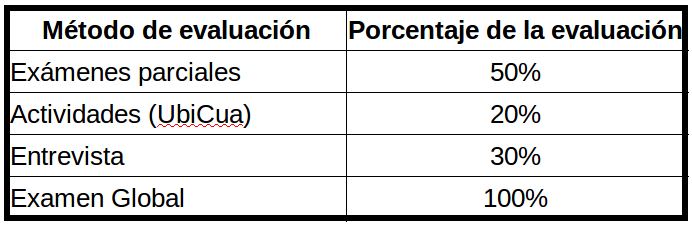
La ponderación de las evaluaciones será según la siguiente tabla
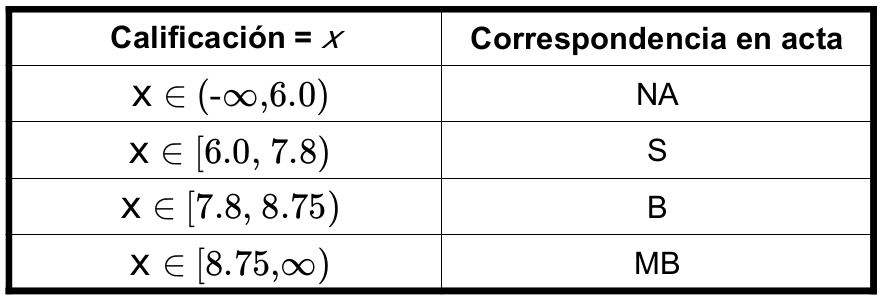
ESCALA DE CALIFICACIÓN
BIBLIOGRAFIA
Además de los libros enlistados a continuación, en la última sección de este curso encontrarás la Biblioteca, donde puedes encontrar más libros de consulta.
- Liesen, J. and Mehrmann, V. (2015). Linear Algebra. Switzerland. Springer International Publishing
- Anton, H. (2001). Introducción al Álgebra Lineal. México. Limusa.
- Lay, D. C. (2007). Álgebra lineal y sus aplicaciones. Pearson Education.
- Lang, S. (2000). Linear Algebra, 3rd Ed.. New York. Springer.
- Friedberg, S., Insel, A. (2014). Linear Algebra, 4th Ed. England. Pearson.
- https://drive.google.com/open?id=1j17BBIGd98f3JxFiVzM17LLi-U2kfrY3