La estructura algebraica de los vectores incluye dos operaciones básicas suma y producto por escalares.
Suma
Si 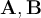${\bf A},{\bf B}$ son vectores, entonces 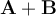${\bf A}+{\bf B}$ es un nuevo vector resultado de la suma de los anteriores.

Producto por escalares
Si 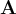${\bf A}$ es un vector y 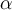$\alpha$ es un escalar, entonces 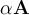$\alpha {\bf A}$  es el vector resultante de multiplicar las cantidades dadas.

Ejemplos:

Las operaciones anteriores satisfacen las siguientes propiedades

Conmutatividad
Dados los vectores 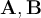${\bf A}, {\bf B}$ entonces ${\bf A}+ {\bf B}={\bf B}+{\bf A}$.

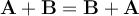Asociatividad sobre la suma
Dados los vectores 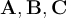${\bf A}, {\bf B}, {\bf C}$ entonces $({\bf A}+ {\bf B})+{\bf C}={\bf A}+({\bf B}+{\bf C})$.

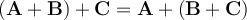Inverso aditivo
Para cada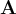${\bf A}$ y el escalar 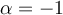$\alpha=-1$, se tiene que  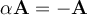$\alpha{\bf A}=-{\bf A}$ es tal que  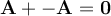${\bf A}+ {-\bf A}={\bf 0}$. Donde el cero es una cantidad vectorial.

Neutro aditivo
Para todo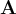${\bf A}$ vector, existe un vector 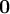${\bf 0}$, llamado vector nulo o vector cero, es tal que 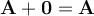${\bf A}+ {\bf 0}={\bf A}$. Donde este vector tiene magnitud nula y cualquier dirección.

Asociatividad sobre el producto de escalares
Dados los escalares 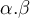$\alpha.\beta$ y el vector 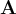${\bf A}$ entonces $\alpha(\beta{\bf A})=(\alpha\beta){\bf A}$.

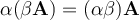Distributividad
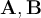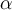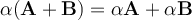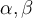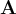Dados ${\bf A}, {\bf B}$ y $\alpha$ entonces $\alpha({\bf A}+ {\bf B})=\alpha{\bf A}+ \alpha{\bf B}$. De manera similar, dados $\alpha, \beta$ y ${\bf A}$ entonces $(\alpha+\beta) {\bf A }= \alpha{\bf A}+\beta {\bf A}$.

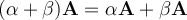Posteriormente  los vectores serán tratados como objetos abstractos que son elementos de un conjunto llamado espacio vectorial.